Question

A tennis coach took his team out for lunch and bought 8 hamburgers and 5 fries for $24. The players were still hungry so the coach bought 6 more hamburgers and 2 more fries for $16.60. Find the cost of each.

Answer 1

Basically this is a systems of equations question. We set up two equations, X is hamburgers Y is fries

8x + 5y = 24
6x + 2y = 16.60

then you solve for each to get your answer.

Answer 2

Answer : The cost of hamburgers and fries is, $2.5 and $0.8

Step-by-step explanation :

Let the cost of hamburgers be, x and the cost of fries be, y.

Thus the two equation will be:

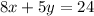`8x+5y=24` ...........(1)

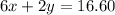`6x+2y=16.60` .............(2)

Using substitution method:

From equation 1 we have to determine the value of 'y'.

`8x+5y=24`

`5y=24-8x`

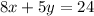
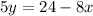
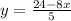`y=(24-8x)/(5)` ........(3)

Now put equation 3 in 2, we get:

`6x+2y=16.60`

`6x+2* ((24-8x)/(5))=16.60`

`6x+((48-16x)/(5))=16.60`

`(30x+48-16x)/(5)=16.60`

`30x+48-16x=83`

`14x=35`

`x=2.5`

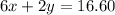
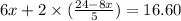
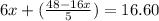
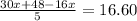
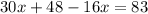
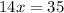
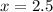
Now put the value of x in equation 3, we get:

`y=(24-8x)/(5)`

`y=(24-8* 2.5)/(5)`

`y=(24-20)/(5)`

`y=(4)/(5)`

`y=0.8`

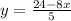
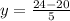
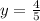
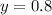
Thus, the cost of hamburgers and fries is, $2.5 and $0.8