Question

A little co fused with net change theorem and displacement distance

Answer 1

If an object moves along a straight line with position s(t), then its velocity is v(t) = s'(t), so

`\int ^3_0v(t)dt=s(t_3)-s(t_0\text{)}`

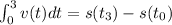
is the net change of position or displacement during time period from t=3 to t=0 seconds.

Lets find the integral of our velocity equation:

`\int ^3_0(-4t+4)dt=(-4(t^2)/(2)+4t)^3_0`

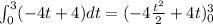
where the last part means the evaluation at t=3 and t=0. Then, we get

`\int ^3_0(-4t+4)dt=-4(3^2)/(2)+4(3)-(-4(0)/(2)+4(0))=-18+12=-6`

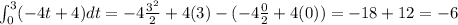
Then, the displacement during time period from t=3 to t=0 seconds is equal to -6 meters