Answer:
option: A
Explanation:
" if for a polynomial with rational coefficients has irrational roots then these irrational roots will always appear in pair " .
we are given that
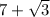 and
and
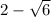 are two roots of a polynomial equation with rational coefficients, then it's complex conjugate is also a root of this polynomial equation i.e. '
are two roots of a polynomial equation with rational coefficients, then it's complex conjugate is also a root of this polynomial equation i.e. '
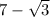 ' and '
' and '
 ' are also roots of this polynomial equation.
' are also roots of this polynomial equation.
Hence, option A is correct.