Answer:
The vertex is (0,0), focus of the parabola is
 , directrix of the parabola is
, directrix of the parabola is
 , focal width is
, focal width is
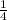 .
.
Explanation:
The given equation of parabola is

It can be written as
 ....(1)
....(1)
The general equation of parabola is
 ... (2)
... (2)
Where, (h,k) is vertex, (h+p,k) is focus, y=h-p is directrix and |4p| is focal width.
On comparing (1) and (2), we get

The vertex is (0,0).
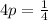
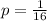
Focus of the parabola is
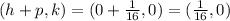
Therefore focus of the parabola is
 .
.
Directrix of the parabola is

Directrix of the parabola is
 .
.
Focal width is
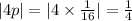
Focal width is
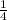 .
.