Question

A bacteria population grows by 10% every 2 years. Presently, the population is 80 000 bacteria. When was the population 25,000? (Can use log if needed but not “in”)

Answer 1

The bacteria population is given by the following formula:

`P(t)=P_0(r)^t`

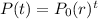
where P0 represents the initial population and r the increasing/decreasing rate and t represents the time. The initial population is given:

`P_0=80000`

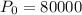
The population grows by 10% every 2 years, therefore, the current population is multiplied by 1.1 every two years. If we consider the unit of time as one year, then, the equation for our bacteria population is:

`P(t)=80000(1.1)^(t/2)`

We want to find the corresponding value for t when P is equal to 25000.

`25000=80000(1.1)^(t/2)`

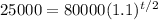
Solving for t, we have:

`\begin{gathered} 25000=80000(1.1)^(t/2) \\ (25000)/(80000)=1.1^(t/2) \\ (5)/(16)=1.1^(t/2) \\ \log(5)/(16)=\log1.1^(t/2) \\ \log5-\log16=(t)/(2)\log1.1 \\ t=2((\log5-\log16)/(\log1.1)) \\ t=2\log_(1.1)(5)/(16) \\ t=-12.2038466... \end{gathered}`