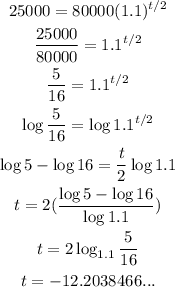The bacteria population is given by the following formula:
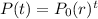
where P0 represents the initial population and r the increasing/decreasing rate and t represents the time. The initial population is given:
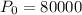
The population grows by 10% every 2 years, therefore, the current population is multiplied by 1.1 every two years. If we consider the unit of time as one year, then, the equation for our bacteria population is:
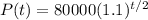
We want to find the corresponding value for t when P is equal to 25000.
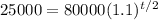
Solving for t, we have: