Question

What is the tenth term of the geometric sequence 3, 6, 12, 24, 48, … ?

Answer 1

You multiply each number by 2 until you get to the tenth term 3*2=6*2=12*2=24 until the tenth term 1,536

Answer 2

Answer: Value of tenth term of the geometric sequence is 1536.

Explanation:

Since we have given that

3, 6, 12, 24, 48, …

Since it is a geometric sequence.

So, here ,

a = first term = 3

r= common ratio is given by

`r=(a_2)/(a_1)\\\\r=(6)/(3)\\\\a=2`

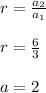
We need to find the tenth term of the geometric sequence.

As we know the formula for "nth term ":

`a_n=ar^(n-1)\\\\Here,\ n=10\\\\a_(10)=3* 2^(10-1)\\\\a_(10)=3* 2^(9)\\\\a_(10)=3* 512\\\\a_(10)=1536`

Hence, Value of tenth term of the geometric sequence is 1536.