Question

Find an equation in standard form for the hyperbola with vertices at (0, ±10) and asymptotes at y=+- 5/4x.

Answer 1

The equation of this hyperbola in standard form:
y² / a² + x² / b² = 1.
y = +/- a/b x
a / b = 5 / 4
a = 10
10 / b = 5 / 4
b = (10 · 4) : 5
b = 8
Answer:
The equation of the hyperbola is:
y² / 100 - x² / 64 = 1

Answer 2

Explanation:

Given that vertex of the hyperbola is

(0,10) and(0,-10)

Hence the hyperbola will have equation of the form

`(y^2)/(a^2) -(x^2)/(b^2) =1`

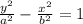
Since vertex has y coordinate as 10, we have a =10

So equation would be
`(y^2)/(10^2) -(x^2)/(b^2) =1`

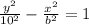
Since asymptotes are y =±5x/4

we have equation of both asymptotes is

`y^2-(25x^2)/(16) =0\\y^2/25-x^2/16 =0\\y^2/100-x^2/64 =0`

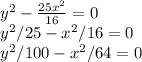
Since hyperbola will have equations same as asymptotes except with difference of constant terms as 1 instead of 0, we have

equation as

`(y^2)/(100) -(x^2)/(64) =1`