Question

The area of a square is found by squaring one of its sides, (A = s2). A certain square has an area of z2 + 18z + 81. Factor the trinomial to find a side of the square.

a. side = z + 27
b. side = z + 18
c. side = z + 9

Answer 1

option c is correct.

side = z+9

Explanation:

Area of a square(A) is given by:

`A = s^2`

where,

s is the side of the square.

As per the statement:

A certain square has an area of
`z^2 + 18z + 81.`

⇒
`A = z^2 + 18z + 81`

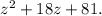
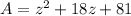
Substitute in [1] we have;

`z^2 + 18z + 81 = s^2`

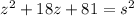
Taking square root both sides we have;

`√(z^2 + 18z + 81) =s`

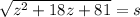
Using identity rule:

`(a+b)^2 =a^2+2ab+b^2`

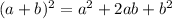
then;

`√(z^2 + 2(1)(9)z + 9^2) =s`

⇒
`√((z+9)^2) =s`

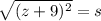
Simplify:

`z+9 = s`

or

s = z+9

Therefore, a side of the square. is, z+9

Answer 2

A = s²
A = z² + 18 z + 81
z² + 18 z + 81 = z² + 9 z + 9 z + 81 = z ( z + 9 ) + 9 ( z + 9 ) =
= ( z + 9 ) ( z + 9 ) = ( z + 9 )²
Answer:
C ) side = z + 9