Answer:
Both right triangles are attached.
To find both similar triangles with a slope of 2/5, we have to remember that slope is related with the tangent of the angle of direction of the line.
So, in each graph, we have angle A, which has the relation:
 ; where
; where
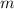 is the slope.
is the slope.
Now, we know by trigonometric reasons that:
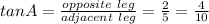
Where the proportion between triangles is 2.