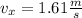Question

Barney walks at a velocity of 1.7 meters/second on an inclined plane, which has an angle of 18.5° with the ground. What is the horizontal component of Barney’s velocity?

Answer 1

(A). 1.6 meters/second

Answer 2

`v_x= 1.61 (m)/(s)`

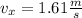
Step-by-step explanation:

Conceptual analysis

Since the velocity has a vector character, in the attached figure we define a rectangular coordinate plane to decompose the total velocity (v) that is in the direction θ with the horizontal.

`v_x` and
`v_y` are the sides of a right triangle that has hypotenuse v.

The total velocity vector is defined as follows:

`v=v_x i+v_y j` Formula (1)

Where:

`v_x` = vcosθ: Formula (2) magnitude of velocity in x direction

`v_y` = vsinθ: Formula (3) magnitude of velocity in y direction

i: is positive (+) to the right of the x axis and negative (-) to the left of the x axis

j: is positive (+) upward of the x axis and negative (-) downward of the y axis

Known data

v = 1.7 m/s

θ = 18.5°

Problem development

We replace the data in formula (2) to calculate the magnitude of
`v_x`:

`v_x=1.7 (m)/(s) * cos(18.5degrees)`

`v_x= 1.61 (m)/(s)`