For a quadratic equation ax²+bx+c, the discriminat is defined the expression:

The value of the discriminant tells us what type and how many roots we have:
0. If the discriminant is greater than 0, we will have two real roots.
,
1. If the discriminant is equal to 0, we will have one (double) real root.
,
2. If the discriminant is less than 0, we will have complex roots.
This can be concluded from the formula for the roots of a quadratic function:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
We can see that the discriminant is the argument of the square root.
Then, if is negative, we will have complex numbers involved and complex roots for the quadratic function. The parabola won't intercept the x-axis.
If the argument is 0, we will have only one value as - 0 = +0. The parabola will be tangent to the x-axis.
Finally, when the argument has a positive value, we will have two values for the roots.
Then, if our disciminant has a value of 4, we have:
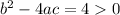
Then, it means that the quadratic polynomial will have 2 real roots.
Answer: There are two real roots.