Answer:
Option (a) is correct.
x = 48.125
Explanation:
Given:
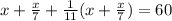
We have to solve for x,
Consider the given expression
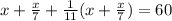
First solving for brackets, we get,
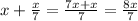
Put , we get,
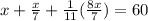
Simplify, we have,
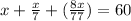
Taking LCM(7,77) = 77
We have,
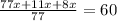
Simplify, we have,
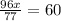
Multiply both side by 77, we have,
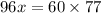
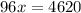
Divide both side by 96, we have,

Thus, x = 48.125
Option (a) is correct.