Question

Assume that a set of test scores is normally distributed with a mean of 100 and a standard deviation of 20. Use the 68-95-99.7 rule to fine the following quantities. a. The percentage of scores less than 100. (round to the one decimal place as needed.)b. The percentage of scores greater than 120.(round to one decimal place as needed. )

Answer 1

We are given that a set of test scores is normally distributed with a mean of 100 and a standard deviation of 20

`\begin{gathered} \mu=100 \\ \sigma=20 \end{gathered}`

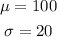
The 68-95-99.7 rule is given by

Approximately, 68% of the values lie within 1 standard deviation away from the mean.

Approximately, 95% of the values lie within 2 standard deviations away from the mean.

Approximately, 97.7% of the values lie within 3 standard deviations away from the mean.

Let us have a look at the curve to better understand the problem

a. The percentage of scores less than 100. (round to the one decimal place as needed.)

As you can see, the normal distribution curve is symmetric about the mean.

Scores less than 100 means the left half of the curve which is 50%

`P(x<100)=34\%+13.5\%+2.35\%+0.15\%=50\%`

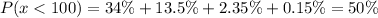
Therefore, scores of less than 100 are 50%

b. The percentage of scores greater than 120. (round to one decimal place as needed.)

Scores greater than 120 lies 1 standard deviation away to the right side of the curve.

So, we need to subtract 34% from the right half of the curve.

`P(x>120)=50\%-34\%=16\%`

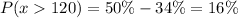
Alternatively,

`P(x>120)=13.5\%+2.35\%+0.15\%=16\%`

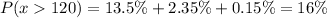
Therefore, scores of greater than 120 are 16%