Question

8. Find the explicit formula for the given sequence. 2, 8, 32, 128, ... a. an = 33 · 4n-1 b. an = 2 · 4n-1 c. an = 8 + 4n-1 32 + 4n-1 d. an

Answer 1

the sequence given is 2, 8, 32 128, .....

the first term = 2

common ratio = the ratio between two successive term we can pick either the 3rd term from the 4th term

the general formula of recursive formula is

`\begin{gathered} a_n=ar^(n-1) \\ a=\text{first term} \\ r=\text{common ratio} \\ n=\text{nth term} \end{gathered}`

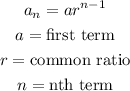
to find the common ratio

we can use the ratio between two successive terms

`\begin{gathered} r=(128)/(32)=4 \\ or \\ r=(32)/(8)=4 \\ \text{the common difference is 4} \end{gathered}`

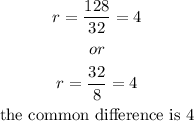
now, we'll proceed to find the recursive formula

`\begin{gathered} a_n=ar^(n-1) \\ a_n=2*4^(n-1) \\ a_n=8^(n-1) \end{gathered}`

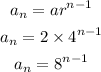
the answer is option b