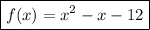Question

2. Write a quadratic function that has -intercepts (- 3, 0) and (4, 0) and passes through the point (5, 8)

Answer 1

`f(x)=x^2-x-12`

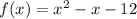
Explanation:

Quadratic Function

Standard Form of Quadratic Function

The standard representation of a quadratic function is:

`f(x)=ax^2+bx+c`

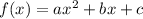
where a,b, and c are constants.

When the zeros of f (x1 and x2) are given, it can be written as:

f(x)=a(x-x1)(x-x2)

Where a is a constant called the leading coefficient.

We are given the two roots of f: x1=-3 and x2=4, thus:

f(x)=a(x+3)(x-4)

We also know that f(5)=8, thus:

f(5)=a(5+3)(5-4)=8

Operating:

a(8)(1)=8

Solving:

a=1

The function is:

f(x)=1(x+3)(x-4)

Operating:

`\boxed{f(x)=x^2-x-12}`