Question

Use the quadratic formula to find the solutions for
y = 3x^3 + 8x - 1

Answer 1

To solve the equation y = 3x^3 + 8x - 1 using the quadratic formula, rewrite the equation in the form ax^2 + bx + c = 0 and apply the quadratic formula.

Step-by-step explanation:

To solve the equation y = 3x^3 + 8x - 1 using the quadratic formula, we first need to rewrite the equation in the form ax^2 + bx + c = 0. In this case, a = 3, b = 8, and c = -1. The quadratic formula is given by x = (-b ± √(b^2 - 4ac)) / 2a. Substituting the values of a, b, and c into the formula gives us x = (-8 ± √(8^2 - 4(3)(-1))) / (2(3)). Simplifying further, we have x = (-8 ± √(64 + 12)) / 6. This gives us two possible solutions: x = (-8 + √76) / 6 and x = (-8 - √76) / 6.

Answer 2

Solving the equation using quadratic formula we get
`\mathbf{x=0.119\:or\:x=-2.785}`

Step-by-step explanation:

We need to use the quadratic formula to find the solutions for

`y = 3x^2 + 8x - 1`

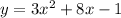
(Note: quadratic formula is used when x^2 is in the equation. So considering 3x^2 instead of 3x^3)

The quadratic formula is:
`x=(-b\pm√(b^2-4ac))/(2a)`

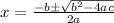
From the given equation
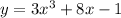`y = 3x^3 + 8x - 1` we have a =3, b=8 and c =-1

Putting values in the formula and finding solutions:

`x=(-b\pm√(b^2-4ac))/(2a)\\x=(-8\pm√((8)^2-4(3)(-1)))/(2(3))\\x=(-8\pm√(64+12))/(6)\\x=(-8\pm√(76))/(6)\\x=(-8\pm8.71)/(6)\\x=(-8+8.71)/(6)\:or\:x=(-8-8.71)/(6)\\x=0.119\:or\:x=-2.785`

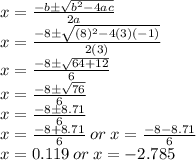
So, Solving the equation using quadratic formula we get
`\mathbf{x=0.119\:or\:x=-2.785}`