Question

If line BD is both the altitude and median of ABC then ABC is

Answer 1

The answer is C./isoceles

Answer 2

Answer: The answer is an isosceles triangle.

Step-by-step explanation: Given that the line BD is both the altitude and median of ΔABC. We are to find the type of the triangle ABC.

In the attached figure, we have drawn BD as the altitude of ΔABC, where D is the mid-ponit of the side AC so that BD is also a median.

Since BD is perpendicular to AC, so triangles ABD and CBD are right-angled triangles.

Therefore, using Pythagoras theorem in ΔABD and ΔCBD, we have

`AB^2=BD^2+AD^2,~~~~~~~~~~~~~~~(i)\\\\AC^2=BD^2+CD^2.~~~~~~~~~~~~~(ii)`

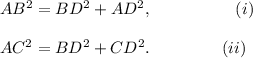
Since D is the mid-point of AC, so AD = CD.

Hence, AD² = CD².

Using this relation in equations (i) and (ii)., we have

`AB^2=AC^2\\\\\Rightarrow AB=AC.`

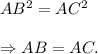
Thus, triangle ABC is an isosceles triangle, since two of its sides are equal.