Question

A production facility employs 20 workers on the day shift, 15 workers on the swing shift, and 10 workers on the graveyard shift. A quality control consultant is to select 6 of these workers for in-depth interviews. Suppose the selection is made in such a way that any particular group of 6 workers has the same chance of being selected as does any other group (drawing 6 slips without replacement from among 45). (Enter your answers to four decimal places.)

Required:
a. How many selections result in all 7 workers coming from the day shift?
b. What is the probability that all 7 selected workers will be from the day shift?
c. What is the probability that all 7 selected workers will be from the same shift?
d. What is the probability that at least two different shifts will be represented among the selected workers?
e. What is the probability that at least one of the shifts will be unrepresented in that sample of workers?

Answer 1

Explanation:

Total number of workers = 20+ 15 + 10 = 45

Suppose 6 workers are selected from 45 workers, the number of ways they can be selected is
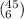`(^(45)_6)` ways

If 7 workers are selected from 20 workers on a day shift;

Then, the number of ways to select 7 members from a group of 20 is
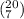`(^(20)_7)` ways;

∴

P( all 7 selected workers will be from the day shift) is:

`= ((^(20)_7))/((^(45)_6))`

`=\frac{ (20!)/(7!(20-7)!) } { (45!)/(6!(45-6)!)}`

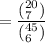
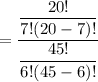
= 0.0095

The possible number of ways to select all day shift workers is:

`=(^(20)_(7))`

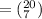
The possible number of ways to select all swing shift workers is:

`=(^(15)_(7))`

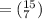
The possible number of ways to select all graveyard shift workers is:

`= ( ^(10)_(7))`

∴

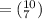
The probability that all selected workers are from the same shift is:

`= \Bigg [ ( (^(20)_7) )/((^(45)_6) ) + ( (^(15)_7) )/((^(45)_6) ) + ( (^(10)_7) )/((^(45)_6) ) \Bigg]`

`= \begin {bmatrix} \frac{ \frac{20!} {7!(20-7)!}}{ ( 45! )/(6!(45-6)!) } + \frac{ \frac{15!} {7!(15-7)!}}{ ( 45! )/(6!(45-6)!) } + \frac{ \frac{10!} {7!(10-7)!}}{ ( 45! )/(6!(45-6)!) } \end {bmatrix}`

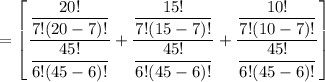
= 0.0095 + 0.00079 + 0.000015

= 0.010305

P(selected workers are from at least two different shifts)

= 1 - P(selected workers are from 1 shift from any of the 3 shifts)

= 1 - 0.010305

= 0.989695

≅ 0.9897

We can determine the probability that at least one shift is unrepresented through the following ways:

Let assume that:

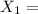`X_1 =` event that day shift is unrepresented

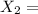`X_2 =` event that swing shift is unrepresented

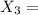`X_3 =` event that graveyard shift is unrepresented

Thus;
`(X_1 \cap X_2)` = event that all of them are drawn from graveyard shift.

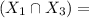`(X_1 \cap X_3) =` event that all are drawn from swing shift

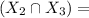`(X_2 \cap X_3) =` event that they are all drawn from day shift.

So;

`P(X_1) = \frac{(^(25)_(7))} { (^(45)_(6)) } = 0.0590`

`P(X_2) = \frac{(^(30)_(7))} { (^(45)_(6)) } = 0.2499`

`P(X_3) = \frac{(^(35)_(7))} { (^(45)_(6)) } = 0.8256`

`P(X_1 \cap X_2) = \frac{(^(10)_(7))} { (^(45)_(6)) } = 0.000015`

`P(X_1 \cap X_3) = \frac{(^(15)_(7))} { (^(45)_(6)) } = 0.00079`

`P(X_2 \cap X_3) = \frac{(^(20)_(7))} { (^(45)_(6)) } = 0.0095`

`P(X_1 \cap X_2 \cap X_3) =0`

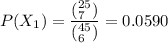
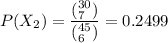
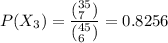
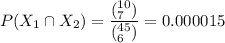
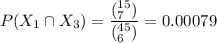
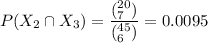
Probability (that at least one shift is unrepresented) is:

`= P(X_1) + P(X_2) +P(X_3) - P(X_1 \cap X_2) - P(X_1 \cap X_3) - P(X_2 \cap X_3) + P(X_1 \cap X_2 \cap X_3)`

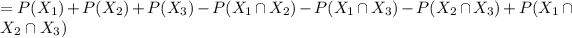
= 0.0590 + 0.2499 + 0.8256 - 0.000015 - 0.00079 - 0.0095 + 0

≅ 1.124