Answer:
There are 50 pages in the book.
Explanation:
Given that:
Martin has read 40% of the book.
Remaining percent = (100 - 40)% = 60%
Number of pages left to finish = 30
Let,
x be the total number of pages in the book.
60% of x = 30
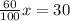
0.6x = 30
Dividing both sides by 0.6
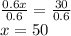
Hence,
There are 50 pages in the book.