Question

Shelby wants to paint the walls and ceiling of a rectangular room

Answer 1

From the given diagram, we get that the surface area of the walls of the rectangular room (without the 5m² for the door and windows) is:

`\text{Area}=2(4.8m+6.8m)\cdot2.6m-5m^2\text{.}`

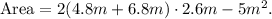
Simplifying the above result we get:

`\begin{gathered} \text{Area}=2(11.6m)\cdot2.6m-5m^2 \\ =60.32m^2-5m^2 \\ =55.32m^2\text{.} \end{gathered}`

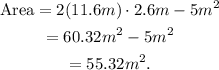
Since one liter of paint covers 9.5m², then Shelby needs:

`(55.32)/(9.5)\approx5.82`

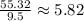
liters of paint.

Therefore, the least amount of paint that Shelby must buy to paint the room is 6 liters.

Now, notice that:

`6=4+1+1.`

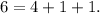
Then Shelby can buy a can of 4L of paint and 2 cans of 1L of paint. Using the given table we get that the paint cost:

`24.95+7.99+7.99=40.93`

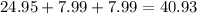
dollars.

Answer:

(a) 6 liters.

(b) $40.93.