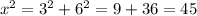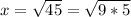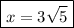Question

Can I get some help on this math problem

Answer 1

`x=3√(5)`

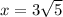
Explanation:

Right Triangles

Right triangles have one of its interior angles with a measure of 90°.

In right triangles the Pythagora's Theorem is satisfied.

Being c the longest side (hypotenuse), a and b the shorter sides (the legs), then:

`c^2=a^2+b^2`

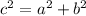
We have modified the image to include some known data. Both triangles are congruent since they share one side, have a right angle, and have the same base length.

This means the value of x can be calculated as the hypotenuse of the triangle 3-6-x:

`x^2=3^2+6^2=9+36=45`

`x=√(45)=√(9*5)`

`\boxed{x=3√(5)}`