Answer:
a.)Point C will be either (4.82, 7.41) or ( -4.82, 2.59)
b.) -x² + 2x + 6y - y² - 5= 0 , 8y - 4x = 11
Explanation:
As given A(2,1,3) and B(0,5,0)
a.)
We have to find C in the xy-plane
⇒ C is of the form (x, y, 0) ( Because in xy plane , z coordinate is zero)
Now, given AB and BC are the legs of the right triangle .
AB = (0, 5, 0) - (2, 1, 3) = ( -2, 4, -3)
BC = (x, y, 0) - (0, 5, 0) = ( x, y-5, 0)
As AB and BC are legs of triangle
⇒AB is perpendicular to BC
⇒(AB).(BC) = 0
⇒( -2, 4, -3).( x, y-5, 0) = 0
⇒ -2x + 4(y-5) -0 = 0
⇒ -2x + 4y- 20 = 0
⇒ -x + 2y- 10 = 0
⇒ 2y = 10 + x
⇒ y = 5 +
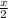 ......(1)
......(1)
As ABC is making an isosceles right triangle
It means two sides of the triangle are equal
Now,
|AB| = √(-2)² + (4)² + (-3)² = √4+16+9 = √29
|BC| = √(x)² + (y-5)² + 0² = √(x)² + (y-5)²
Now,
AS AB = BC
⇒|AB| = |BC|
⇒|AB|² = |BC|²
⇒29 = (x)² + (y-5)²
⇒29 = (x)² + (5 +
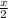 -5)²
-5)²
⇒29 = (x)² + (
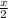 )²
)²
⇒29 = x²( 1 +
 ) = x²(
) = x²(
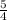 )
)
⇒ x² =
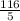 = 23.2
= 23.2
⇒ x = 4.82 , -4.82
⇒y = 7.41 , 2.59
so, Point C will be either (4.82, 7.41) or ( -4.82, 2.59)
b.)
As given AB is the hypotenuse of the right triangle
S, AC and CB will perpendicular to each other
Now,
AC = (x, y, 0) - ( 2, 1, 3) = ( x-2, y-1, -3)
CB = (0, 5, 0) - (x, y, 0) = (-x, 5-y, 0)
As, AC and CB is perpendicular
⇒(AC).(CB) = 0
⇒( x-2, y-1, -3).(-x, 5-y, 0) = 0
⇒(x-2)(-x) + (y-1)(5-y) - 0 = 0
⇒-x² + 2x + 5y - y² - 5 + y = 0
⇒-x² + 2x + 6y - y² - 5= 0 ..........(2)
As ABC is making an isosceles right triangle
It means two sides of the triangle are equal
Now,
|AC| = √(x-2)² + (y-1)² + (0-3)² = √(x-2)² + (y-1)² + 9
|BC| = √(x)² + (y-5)² + 0² = √(x)² + (y-5)²
Now,
AS AC = BC
⇒|AC| = |BC|
⇒|AC|² = |BC|²
⇒(x-2)² + (y-1)² + 9 = (x)² + (y-5)²
⇒x² + 4 - 4x + y² + 1 - 2y + 9 = x² + y² + 25 - 10y
⇒ 4 - 4x + 1 - 2y + 9 = 25 - 10y
⇒14 - 4x - 2y = 25 - 10y
⇒10y - 2y - 4x = 25 - 14
⇒8y - 4x = 11 ........(3)
Now, we have 2 equations
-x² + 2x + 6y - y² - 5= 0 , 8y - 4x = 11
Solve these equations to find x, y