Answer:
Option A, B and C are the correct options.
Explanation:
Inequality has been given as 6x ≥ 3 + 4(2x - 1)
By solving it further,
6x ≥ 3 + 8x - 4 [Option B is the correct option]
6x ≥ 8x - 1
6x - 8x ≥ 8x - 1 - 8x
-2x ≥ -1
2x ≤ 1
1 ≥ 2x [Option A is the correct option]
x ≤
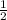
Option C represents the inequality drawn on the number line.
Therefore, Options A, B and C are the correct options.