Question

A fossilized leaf contains 15% of its normal amount of carbon 14. How old is the fossil (to the nearest year)? Use 5600 years as the half-life of carbon 14. Solve the problem.

A. 35,828
B. 15,299
C. 1311
D. 21,839

Answer 1

I had this same question. The answer is b. 15,299.
hope this helps.

Answer 2

Option B - 15299

Explanation:

Given : A fossilized leaf contains 15% of its normal amount of carbon 14. Use 5600 years as the half-life of carbon 14.

To find : How old is the fossil (to the nearest year)?

Solution :

Let the normal or initial amount of carbon be A,

According to the question,

An exponential function form
`f(t)=ab^t`

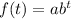
Where, a is the initial i.e, a=A

A fossilized leaf contains 15% of its normal amount of carbon 14.

So, f(t)=15% of A

i.e,
`f(t)=0.15A`

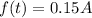
b is half-life of Carbon-14 b=0.5

and t is the time span or age of the fossil in years.

Substitute all the values in the formula,

`0.15A=A(0.5)^t`

`(0.15A)/(A)=(0.5)^t`

`0.15=(0.5)^t`

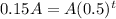
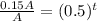
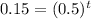
Taking log both side,

`\log(0.15)=t\log(0.5)`

`t=(\log(0.15))/(\log(0.5))`

`t=2.73`

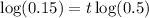
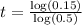
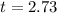
For 5600 years the age of the fossil is
`t=2.73* 5600=15288`

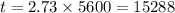
Therefore, Approximately Option B is correct.

The fossils are 15299 years old.