Answer:
option (b) is correct.
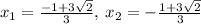
Explanation:
Given equation
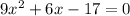
We have to solve the given quadratic equation using quadratic formula.
For the given standard quadratic equation
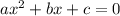
Quadratic formula is given as
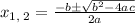
Comparing with given quadratic equation, we have a = 9, b = 6 and c = -17
Substitute in quadratic formula, we have,
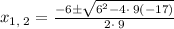
Simplify , we have
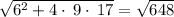
we get,

Also,
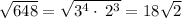
we have,

Thus, seperating both facotors, we have,
 and
and

Simplify, both we get,
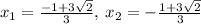
Thus, option (b) is correct.