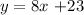Question

7. Write an equation in slope–intercept form for a line that passes through thepoint (–2, 7) and is parallel to y = 8x + 9.

Answer 1

Step-by-step explanation:

The slope-intercept form of a line with slope m and y-intercept b is given by the following equation:

`y\text{ = mx+b}`

Let us denote by L1 the parallel line to the line L that we want to find.

L1 is given by the following equation in slope-intercept form:

`y\text{ = 8x + 9}`

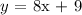
where the slope m = 8 and the y-intercept b = 9.

Now, to find the equation of L we can perform the following steps:

Step 1: Find the slope of L:

Slopes of parallel lines are equal, thus the slope of L1 is equal to the slope of L. Then, the slope m of L is:

`m\text{ = 8}`

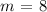
Step 2: Write the provisional equation of the line L in the slope-intercept form:

According to the previous step we have:

`y\text{ = 8x+b}`

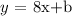
Step 3: Find the y-intercept b of L:

Take any point on the line L and replace its coordinates (x,y) in the previous equation, then solve for b.

According to the problem, the line L passes through the point (–2, 7), thus we can take the point (x,y)=(-2,7):

`7\text{= 8\lparen -2\rparen+b}`

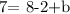
this is equivalent to:

`7\text{ = -16 +b}`

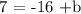
solving for b, we obtain:

`b=\text{ 7 + 16 = 23}`

then

`b=23`

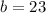
Step 4: Write the equation of the line L in the slope-intercept form:

According to the previous steps we have that:

m = 8

b = 23

then, we can conclude that the equation of the line L in the slope-intercept form is:

`y=8x\text{ +23}`

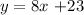
and we can conclude that the answer is:

Answer:

`y=8x\text{ +23}`