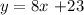Step-by-step explanation:
The slope-intercept form of a line with slope m and y-intercept b is given by the following equation:
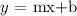
Let us denote by L1 the parallel line to the line L that we want to find.
L1 is given by the following equation in slope-intercept form:
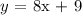
where the slope m = 8 and the y-intercept b = 9.
Now, to find the equation of L we can perform the following steps:
Step 1: Find the slope of L:
Slopes of parallel lines are equal, thus the slope of L1 is equal to the slope of L. Then, the slope m of L is:
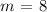
Step 2: Write the provisional equation of the line L in the slope-intercept form:
According to the previous step we have:
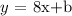
Step 3: Find the y-intercept b of L:
Take any point on the line L and replace its coordinates (x,y) in the previous equation, then solve for b.
According to the problem, the line L passes through the point (–2, 7), thus we can take the point (x,y)=(-2,7):
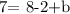
this is equivalent to:
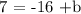
solving for b, we obtain:
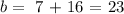
then
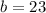
Step 4: Write the equation of the line L in the slope-intercept form:
According to the previous steps we have that:
m = 8
b = 23
then, we can conclude that the equation of the line L in the slope-intercept form is:
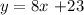
and we can conclude that the answer is:
Answer: