Question

A metallurgist has one alloy containing 45% copper and another containing 69 % copper. How many pounds of each alloy must he use to make 42 pounds of a third alloy containing 66 % copper? (Round to two decimal places if necessary.)

Answer 1

Let x be the pounds of 45% copper alloy

Let y be the pounds of 69% copper alloy

To get the amount of copper in a alloy you multiply the pounds of it by the % of copper in decimal form.

Use 0.45x and 0.69y to get a alloy of 42*0.66 (42 pounds containig 66% copper)

`\begin{gathered} 0.45x+0.69y=42\cdot0.66 \\ \\ 0.45x+0.69y=27.72 \end{gathered}`

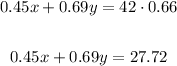
x and y needs to sum the pounds in the last alloy:

`x+y=42`

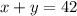
Use the next system of equations to solve the given problem:

`\begin{gathered} 0.45x+0.69y=27.72 \\ x+y=42 \end{gathered}`

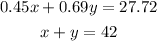
1. Solve y in the second equation:

`y=42-x`

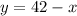
2. Substitute the y in the first equation by the value you get in first step:

`0.45x+0.69(42-x)=27.72`

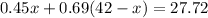
3. Solve x:

`\begin{gathered} 0.45x+28.98-0.69x=27.72 \\ -0.24x+28.98=27.72 \\ -0.24x=27.72-28.98 \\ -0.24x=-1.26 \\ x=(-1.26)/(-0.24) \\ \\ x=5.25 \end{gathered}`

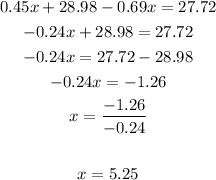
4. Use the value of x to solve y:

`\begin{gathered} y=42-x \\ y=42-5.25 \\ y=36.75 \end{gathered}`

Solution: x=5.25, y=36.75

Then, the metallurgist must use 5.25 pounds of the alloy containing 45% copper and 36.75 pounds of the alloy containing 69% copper