Question

The line CD passes through the points C (2.-1) and D (1, 1). Which of the

following represents the equation of the line in Point-Slope Form?*

Answer 1

The equation of the line in Point-Slope Form will be:

`y + 1 = -2(x - 2)`

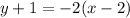
Also, check the attached graph below.

Explanation:

Given the points

• C(2, -1)

• D(1, 1)

Determining the slope between the points C (2.-1) and D (1, 1).

• (x₁, y₁) = (2, -1)

• (x₂, y₂) = (1, 1)

Using the formula

Slope = m = [y₂ - y₁] / [x₂ - x₁]

= [1 - (-1)] / [1 - 2]

= [1+1] / [-1]

= [2] / [-1]

= -2

Thus, the slope of the line = m = -2

The point-slope form of the line equation is defined as

`y-y_1=m\left(x-x_1\right)`

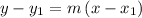
where

• m is the slope of the line

• (x₁, y₁) is the point

In our case:

• (x₁, y₁) = (2, -1)

• m = -2

substituting the values m = -2 and the point (x₁, y₁) = (2, -1) in the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

`y - (-1) = -2 (x - 2)`

`y + 1 = -2(x - 2)`

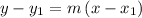
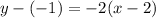
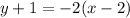
Therefore, the equation of the line in Point-Slope Form will be:

`y + 1 = -2(x - 2)`

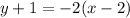
Also, check the attached graph below.