Question

Someone plssss help (15 points) ty

Answer 1

`\color{plum}\bold{x \tt \: = 67}`

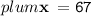
Steps to derive the correct solution :

∠63° and ∠(2x-17)° are a linear pair, so their sum will be equal to 180°.

Which means :

`= 63 + 2x - 17 = 180`

`= 63 + 2x = 180 + 17`

`= 63 + 2x = 197`

`= 2x = 197 - 63`

`= 2x = 134`

`= x = 67`

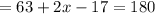
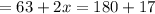
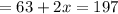
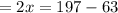
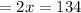
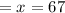
Let us place 67 in the place of x and see if the substitution is equivalent to 180° :

`= 63 + 2 * 67 - 17 = 180`

`= 63 + 134 - 17 = 180`

`= 63 + 117 = 180`

`= 180 = 180`

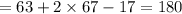
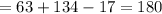
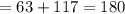
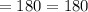
Thus, the value of x we found out is correct.

Therefore, x = 67

Answer 2

x = 67

Explanation:

2x - 17 + 63 = 180 {Linear pair}

2x + 46 = 180

2x = 180 - 46

2x = 134

x = 134/2

x = 67