Question

Suppose the average monthly mortgage payment in the U.S. is $982, the standard deviation is $180, and the mortgage payments are approximately normally distributed. Find the probability that a randomly selected mortgage payment is between $877 and $1,042.

Answer 1

The formula for z-score is given as

`z=(x-\mu)/(\sigma)`

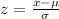
we will have to calculate two values of the z-scores

The given values are

`\begin{gathered} x_1=\text{ \$877} \\ \mu_1=\text{ \$982} \\ \sigma_1=\text{ \$180} \end{gathered}`

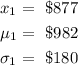
By substitution, we will have

`\begin{gathered} z_1=\text{ }\frac{\text{\$877- \$982}}{\text{ \$180}} \\ z_1=\text{ }\frac{\text{-\$105}}{\text{ \$180}} \\ z_1=-\text{ 0.5833} \end{gathered}`

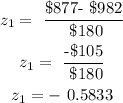
we will then calculate the second z-score

The given values are

`\begin{gathered} x_2=\text{ \$1042} \\ \sigma_2=\text{ \$180} \\ \mu_2=\text{ \$982} \end{gathered}`

By substitution, we will have

`\begin{gathered} z_2=\frac{\text{ \$1042 - \$982}}{\text{ \$180}} \\ z_2=\text{ }\frac{\text{60}}{180} \\ z_2=0.3333 \end{gathered}`

P(-0.5833 ≤ z ≤ 0.3333) = 0.3507

Hence the probability that a randomly selected mortgage payment is between $877 and $1,042 is 0.3507