Question

The following data give the estimated prices of a 6-ounce can or a 7.06-ounce pouch of water-packed tuna for 14 different brands, based on prices paid nationally in supermarkets are reproduced here.

0.99 1.92 1.23 0.85 0.65 0.53 1.41
1.12 0.63 0.67 0.69 0.60 0.60 0.66

a. Find the range.
b. Find the sample variance.
c. Find the sample standard deviation.

Answer 1

a) Range = 1.39

b) the sample variance is 0.1597

c) the sample standard deviation is 0.3996

Explanation:

Given the data in the question;

a) Find the range.

To determine the range, we simple subtract the smallest value from the largest value. i.e

Range = largest value - smallest value

from data set; our smallest is 0.53 while our largest value is 1.92

so

Range = 1.92 - 0.53 = 1.39

b) Find the sample variance.

To determine our variance, we use the following formula;

∑(
`X_(i)` -
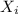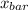`x_(bar)`)² / n - 1 = [ ∑
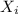`X_(i)`²/n-1 ] - [
`(n)/(n-1)`(
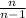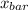`x_(bar)`)²]

where
`x_(bar)` = ∑
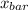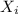`X_(i)`/n

n is sample size = 14 so lets calculate ∑
`X_(i)`

∑
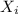
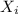`X_(i)` = 0.99 + 1.92 + 1.23 + 0.85 + 0.65 + 0.53 + 1.41 + 1.12 + 0.63 + 0.67 + 0.69 + 0.60 + 0.60 + 0.66

∑
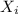`X_(i)` = 12.55

∑
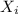`X_(i)`² = 0.99² + 1.92² + 1.23² + 0.85² + 0.65² + 0.53² + 1.41² + 1.12² + 0.63² + 0.67² + 0.69² + 0.60² + 0.60² + 0.66²

∑
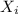`X_(i)`² = 13.3253

so

our
`x_(bar)` = ∑
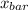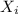`X_(i)`/n = 12.55 / 14 = 0.8964

so our Variance will be;

= [ ∑
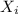`X_(i)`²/n-1 ] - [
`(n)/(n-1)`(
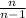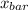`x_(bar)`)²]

= [ 13.3253 / 14-1 ] - [
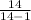`(14)/(14-1)` (0.8964)²]

= 1.025 - 0.8653

= 0.1597

Therefore, the sample variance is 0.1597

c) Find the sample standard deviation.

we know that standard deviation is the square root of variance;

standard deviation = √Variance

standard deviation = √0.1597

standard deviation = 0.3996

Therefore, the sample standard deviation is 0.3996