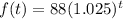Answer:
The population model of wolves after t years is given by
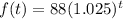
D is the correct option.
Explanation:
The exponential function can be represented as
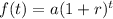
a = initial amount
r = rate
t = time
Now, we have been given that
r = 2.5% = 0.025
a = 88
On substituting these values in the above exponential model
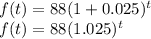
The population model of wolves after t years is given by