Question

A rocket is fired with an initial vertical velocity of 40 m/s from a launch pad 45 m high, and its height is given by the formula -5t^2+40t+45 where h is in meters and t is in seconds. How high does the rocket go? How much time is the rocket in flight?

Answer 1

Given:

The height h is given by the formula:

`\begin{gathered} h=-5t^2\text{ +40t +45} \\ h\text{ is in meters} \\ t\text{ is in seconds} \end{gathered}`

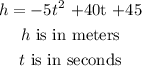
height of the launch pad = 45m

To find the height the rocket goes, we take the first derivative of the function h and then set it to zero

`h^(\prime)^{}\text{= -10t + 40}`
`\begin{gathered} h^(\prime)\text{ = 0} \\ -10t\text{ + 40 = 0} \\ -10t\text{ = -40} \\ \text{Divide both sides by -10} \\ t\text{ = 4} \end{gathered}`

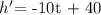
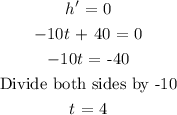
The height the rocket travels is thus:

`\begin{gathered} h(t=4)=-5(4)^2\text{ + 40(4) + 45} \\ =\text{ 125 m} \end{gathered}`

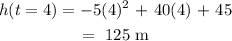
Hence, the rocket goes as high as :

`\begin{gathered} =\text{ 125 - 45} \\ =\text{ 80 m} \end{gathered}`

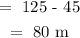
We have subtracted the height of the launch pad so that we can get the actual height the rocket travels

The time the rocket takes in flight is two times the time it takes to reach the top :

`\begin{gathered} \text{time = 2 }*\text{ 4} \\ =\text{ 8s } \end{gathered}`

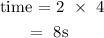
Answer summary

height the rocket travels = 80m

the time the rocket is in flight = 8s