Question

Find the derivative by the limit process f(x)=7

Answer 1

`f'(x) = 0`

General Formulas and Concepts:

Algebra I

Functions

• Function Notation

Calculus

Limits

Differentiation

• Derivatives
• Derivative Notation
• Definition of a Derivative:
  `\displaystyle f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h)`

Explanation:

Step 1: Define

Identify

`\displaystyle f(x) = 7`

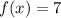
Step 2: Differentiate

1. Substitute in function values [Definition of a Derivative]:
   `\displaystyle f'(x) = \lim_(h \to 0) (7 - 7)/(h)`
2. Simplify:
   `\displaystyle f'(x) = \lim_(h \to 0) (0)/(h)`
3. Evaluate limit:
   `\displaystyle f'(x) = 0`

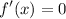
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation