Question

Need help with a question

Answer 1

Recall that the product rule of exponents is given by

`a^x\cdot a^y=a^(x+y)`

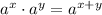
Recall that the quotient rule of exponents is given by

`(a^x)/(a^y)=a^(x-y)`

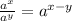
Recall that the negative rule of exponents is given

Expression 1:

Let us apply the product rule of exponents to the expression

`2^(-2)\cdot2^(-2)=2^(-2+(-2))=2^(-2-2)=2^(-4)`

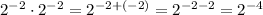
Now let us apply the negative rule of exponents to the above expression

`2^(-4)=(1)/(2^4)`

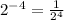
Therefore, the 1st expression matches with the 5th answer.

Expression 2:

Let us apply the product rule of exponents to the expression

`2^(-2)\cdot2^2=2^(-2+2)=2^0=1`

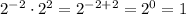
Please note that any number having an exponent of 0 is equal to 1

Therefore, the 2nd expression matches with the 3rd answer

Expression 3:

Let us apply the product rule of exponents to the expression

`2^4\cdot2^(-5)=2^(4+(-5))=2^(4-5)=2^(-1)`

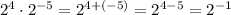
Now let us apply the negative rule of exponents to the above expression

`2^(-1)=(1)/(2)`

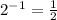
Therefore, the 3rd expression matches with the 2nd answer.

Expression 4:

Let us apply the quotient rule of exponents to the expression

`(2^8)/(2^2)=2^(8-2)=2^6`

Therefore, the 4th expression matches with the 6th answer.

Expression 5:

Let us apply the quotient rule of exponents to the expression

`(2^3)/(2^(12))=2^(3-12)=2^(-9)`

Now let us apply the negative rule of exponents to the above expression

`2^(-9)=(1)/(2^9)`

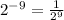
Therefore, the 5th expression matches with the 1st answer.

Expression 6:

Let us apply the quotient rule of exponents to the expression

`(2^(10))/(2^6)=2^(10-6)=2^4`

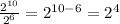
Therefore, the 6th expression matches with the 4th answer.