Question

Which ordered pairs are solutions to the inequality y−2x≤−3?

Select each correct answer.

(5, −3)(5, −3)

(0, −2)(0, −2)

(−6, −3)(−6, −3)

(1, −1)(1, −1)

(7, 12)

Answer 1

Answer:(5, −3),(1, −1)

Explanation:

Answer 2

we will proceed to resolve each case to determine the solution

we have

`y-2x \leq -3`

`y\leq2x-3`

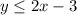
we know that

If an ordered pair is the solution of the inequality, then it must satisfy the inequality.

case a)
`(5,-3)`

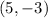
Substitute the value of x and y in the inequality

`-3\leq2*5-3`

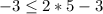
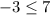`-3\leq7` -------> is true

so

The ordered pair
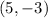`(5,-3)` is a solution

case b)
`(0,-2)`

Substitute the value of x and y in the inequality

`-2\leq2*0-3`

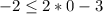
`-2\leq-3` -------> is False

so

The ordered pair
`(0,-2)` is not a solution

case c)
`(-6,-3)`

Substitute the value of x and y in the inequality

`-3\leq2*-6-3`

`-3\leq-15` -------> is False

so

The ordered pair
`(-6,-3)` is not a solution

case d)
`(1,-1)`

Substitute the value of x and y in the inequality

`-1\leq2*1-3`

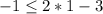
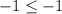`-1\leq-1` -------> is True

so

The ordered pair
`(1,-1)` is a solution

case e)
`(7,12)`

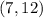
Substitute the value of x and y in the inequality

`12\leq2*7-3`

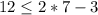
`12\leq11` -------> is False

so

The ordered pair
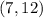`(7,12)` is not a solution

Verify

using a graphing tool

see the attached figure

the solution is the shaded area below the line

The points A and D lies on the shaded area, therefore the ordered pairs A and D are solution of the inequality