Question

Assume the random variable X is normally distributed, with a mean of 56 and a standard deviation of 6. Find the 11th percentile(Round to two decimal places as needed)

Answer 1

The 11th percentile is 48.64

SOLUTION

Problem statement

We are told to find the 11th percentile of a random variable X that is normally distributed with a mean of 56 and a standard deviation of 6.

Method

- The percentile represents the probability that variable X will take a particular value; only that the probability has been multiplied by 100% to make it a percentile.

- This implies that:

`\begin{gathered} 11th\text{ percentile}=11\text{ \%} \\ \\ \therefore\text{The probability associated with the }11th\text{ percentile}=(11)/(100)=0.11 \end{gathered}`

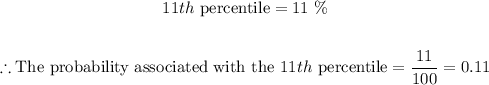
- The normal distribution gives us a probability density curve with the mean at its center, the values of variable X on the x-axis while the corresponding Z-score is shown on the y-axis.

- Thus, the probability of 0.11 tells us that the area under the probability density curve is 0.11 and we are looking for the value of X that corresponds to this area of 0.11.

This is illustrated below:

- Thus, to find the value of X that corresponds to the 11th percentile (or Area under the curve of 0.11), we follow these steps:

1. Find the left-hand side Z-score that corresponds to the probability of 0.11.

2. Apply the Z-score formula to find the value of X. The Z-score formula is given by:

`\begin{gathered} Z=(X-\mu)/(\sigma) \\ \\ \text{where,} \\ \mu=\text{Population mean} \\ \sigma=\text{Population standard deviation} \end{gathered}`

Let us apply these steps and find the value of X.

Implementation

Step 1:

Find the left-hand side Z-score:

We shall find this Z-score using Z-score tables as shown below:

- From the above figure, we can observe that the probability 0.11 lies between a Z-score of -1.22 and -1.23.

- We can decide the exact number using interpolation or by using an online Z-score calculator.

- Using an online Z-score calculator, we have that Z(0.11) = - 1.227.

Step 2: Apply the Z-score formula:

`\begin{gathered} Z=(X-\mu)/(\sigma) \\ \\ \mu=56,\sigma=6,Z=-1.227 \\ \\ \therefore-1.227=(X-56)/(6) \\ \\ \text{ Multiply both sides by 6} \\ \\ -1.227(6)=X-56 \\ -7.362=X-56 \\ \\ \text{Add 56 to both sides} \\ \\ X=56-7.362 \\ \\ \therefore X=48.638\approx48.64\text{ (To two decimal places)} \end{gathered}`

Final Answer

The 11th percentile is 48.64