Solution
The problem is under binomial distribution probability.
The formula to be used is shown below
Fot the question before us,
n = 6
x = 2
p = 1 - 95% = 1 - 0.95 = 0.05
q = 95% = 0.95
Sunstituting the values into the above formula, we have
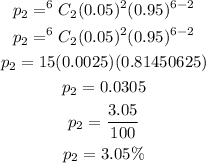
The answer is 3.05%