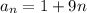According to the given problem,
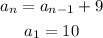
Solve for the successive terms by substituting n=2,3,4,5,....
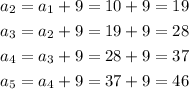
So the sequence is obtained as,
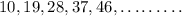
Onserve that this is an Arithmetic Progression with first term (a) 10, and the common difference (d) 9 units.
So the nth term of the AP is given by,
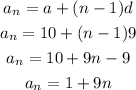
This the explicit formula representing the sequence is obtained as,