Question

Write an explicit formula that represents the sequence defined by the followingrecursive formula:a1 = 10 and an = an-1 + 9

Answer 1

According to the given problem,

`\begin{gathered} a_n=a_(n-1)+9 \\ a_1=10 \end{gathered}`

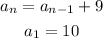
Solve for the successive terms by substituting n=2,3,4,5,....

`\begin{gathered} a_2=a_1+9=10+9=19 \\ a_3=a_2+9=19+9=28 \\ a_4=a_3+9=28+9=37 \\ a_5=a_4+9=37+9=46 \end{gathered}`

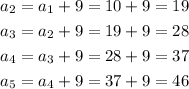
So the sequence is obtained as,

`10,19,28,37,46,\ldots\ldots\ldots`

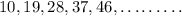
Onserve that this is an Arithmetic Progression with first term (a) 10, and the common difference (d) 9 units.

So the nth term of the AP is given by,

`\begin{gathered} a_n=a+(n-1)d \\ a_n=10+(n-1)9 \\ a_n=10+9n-9 \\ a_n=1+9n \end{gathered}`

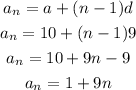
This the explicit formula representing the sequence is obtained as,

`a_n=1+9n`