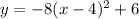vertex form is
y=a(x-h)^2+k
vertex is (h,k)
axis of symmetry is x=4, therfor h=4
y=a(x-4)^2+k
we have some points
(3,-2) and (6,-26)
input and solve for a and k
(3,-2)
-2=a(3-4)^2+k
-2=a(-1)^2+k
-2=a(1)+k
-2=a+k
(6,-26)
-26=a(6-4)^2+k
-26=a(2)^2+k
-26=a(4)+k
-26=4a+k
we have
-2=a+k
-26=4a+k
multiply first equation by -1 and add to second
2=-a-k
-26=4a+k +-24=3a+0k
-24=3a
divide both sides by 3
-8=a
-2=a+k
-2=-8+k
add 8 to both sides
6=k
the equation is