Question

How many real and complex roots exist for the polynomial F(x) = x2 + 2x2 + 4x+8 ?

Answer 1

Given:

`f(x)=x^3+2x^2+4x+8`

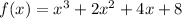
Let this as equation

`x^3+2x^2+4x+8=0`

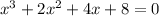
Set x=-1, we get

`(-1)^3+2(-1)^2_{}+4(-1)+8=0`

`-1+2-4+8=0`

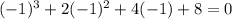
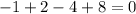
x=-1 is not a root.

Set x=-2, we get

`(-2)^3+2(-2)^2_{}+4(-2)+8=0`

`-8+8+-8+8=0`

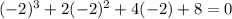
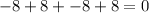
x=-2 is a root that is a real root.

Using a synthetic method to find the remaining roots.

The equation can be written as follows.

`x^2+4=0`
`x^2=-4`
`x=\pm2i`

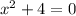
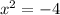
x=2i and x=-2i are complex roots.

Hence we get one real root and two complex roots.