Question

For Which Value of P and W is P+W a rational number. Tell me how you got that answer

1) P= 1/ square root of 3 and W=1/square root of 6
2)P=1/ square root of 4 and W=1/square root of 9
3)P=1/square root of 6 and W=1/square root of 10
4)P=1/square root of 25 and W=1/square root of 2

Answer 1

300.02 if you use the square root of 72

Answer 2

Option 2 - P=1/ square root of 4 and W=1/square root of 9

Explanation:

To find : For Which Value of P and W is P+W a rational number ?

Solution :

Solving each expression,

1) P= 1/ square root of 3 and W=1/square root of 6

i.e.
`P=(1)/(√(3))` and
`W=(1)/(√(6))`

`P+W=(1)/(√(3))+(1)/(√(6))`

`P+W=(\sqrt2+1)/(√(6))`

`P+W=0.985598559...`

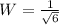
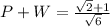
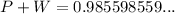
It is an irrational number.

2) P=1/ square root of 4 and W=1/square root of 9

i.e.
`P=(1)/(√(4))` and
`W=(1)/(√(9))`

`P+W=(1)/(√(4))+(1)/(√(9))`

`P+W=(1)/(2)+(1)/(3)`

`P+W=(5)/(6)`

`P+W=0.833333.....`

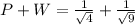
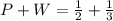
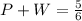
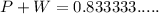
It is a rational number as repeating decimal.

3) P=1/square root of 6 and W=1/square root of 10

i.e.
`P=(1)/(√(6))` and
`W=(1)/(√(10))`

`P+W=(1)/(√(6))+(1)/(√(10))`

`P+W=(\sqrt5+\sqrt3)/(√(30))`

`P+W=0.724476056.....`

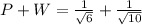
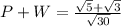
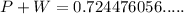
It is an irrational number.

4) P=1/square root of 25 and W=1/square root of 2

i.e.
`P=(1)/(√(25))` and
`W=(1)/(√(2))`

`P+W=(1)/(5)+(1)/(√(2))`

`P+W=(\sqrt2+5)/(5√(2))`

`P+W=0.9071067811.....`

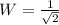
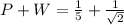
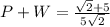
It is an irrational number.

Therefore, Option 2 is correct.