Question

If the Longer leg of a 30 60 90 degree and the base of the triangle has a length of 51 centimeters, what is the length of the shorter leg?

Answer 1

We have the following triangle:

Since the base is equal to 51 cm, we can find the other side by using the tangent functions.

For instance,

`\tan 60=(x)/(51)`

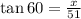
hence, we can isolate x as

`x=51\cdot\tan 60`

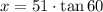
now, tan 60 = 1.73, therefore, we have

`\begin{gathered} x=51\cdot1.73 \\ x=88.33 \end{gathered}`

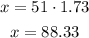
and the other side is equal to 88.33 centimeters. Since the hypotenuse is always the largest side and is in front of the right angle, the shorter leg is equal to 51 centimeters.