Solution
- The question gives us the following expression to solve
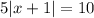
- Before we proceed, we should get rid of the 5 multiplying the absolute value function. This would enable us to work directly with the absolute value function and make our work a lot easier.
- To get rid of the 5, we can simply divide both sides by 5. This is done below:
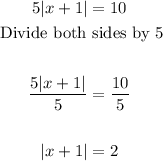
- Now, we can work directly with the absolute value function.
- The absolute value function has the property that
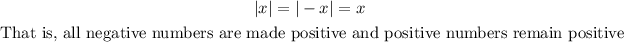
- We can apply this rule to the question. Based on what we have discussed so far, we can conclude that the number or expression (x + 1) inside the absolute value function can either be positive or negative and they would still give us a positive 2 as a result.
- Thus, we can say:
![\begin{gathered} x+1=2 \\ \text{ OR} \\ x+1=-2 \\ \\ \text{ To be sure that these are the two possibilities, we can take the absolute value of both sides for the two} \\ \text{ expressionis} \\ That\text{ is,} \\ \\ |x+1|=|2|=2 \\ OR \\ |x+1|=|-2|=2 \end{gathered}]()
- We can see that both expressions give us back the question. This means we just need to solve the two expressions and find the two possible values of x.
- This is done below:
![undefined]()