Question

Solve the following absolute value equation 5|x+1|=10x=_x=_enter the negative solution first

Answer 1

- The question gives us the following expression to solve

`5|x+1|=10`

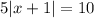
- Before we proceed, we should get rid of the 5 multiplying the absolute value function. This would enable us to work directly with the absolute value function and make our work a lot easier.

- To get rid of the 5, we can simply divide both sides by 5. This is done below:

`\begin{gathered} 5|x+1|=10 \\ \text{ Divide both sides by 5} \\ \\ (5|x+1|)/(5)=(10)/(5) \\ \\ |x+1|=2 \end{gathered}`

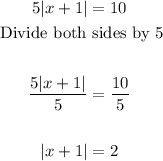
- Now, we can work directly with the absolute value function.

- The absolute value function has the property that

`\begin{gathered} |x|=|-x|=x \\ \text{ That is, all negative numbers are made positive and positive numbers remain positive} \end{gathered}`

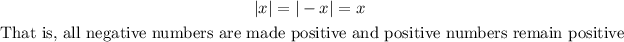
- We can apply this rule to the question. Based on what we have discussed so far, we can conclude that the number or expression (x + 1) inside the absolute value function can either be positive or negative and they would still give us a positive 2 as a result.

- Thus, we can say:

- We can see that both expressions give us back the question. This means we just need to solve the two expressions and find the two possible values of x.

- This is done below: