Answer:
Option B - 65%
Explanation:
Given : Suppose the x-axis of a density graph represents someone's height in inches. If the area under the density curve from 60 inches to 70 inches is 0.65.
To find : What is the probability of someone's height being anywhere from 60 inches to 70 inches?
Solution :
The probability percentage of a curve is defined as the area under the density curve as
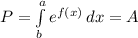
The area under the density curve from 60 inches to 70 inches is 0.65.
So,The probability is equal to the area = 0.65
Therefore, The probability of someone's height being anywhere from 60 inches to 70 inches is 65%.
Hence, Option B is correct.