Question

A certain game consists of rolling a single fair die and pays off as follows: $6 for a 6, $4 for a 5, $1 for a 4, and no payoff otherwise. Find the expected winnings for this game.

Answer 1

The expected winnings are given by the following formula:

`E(x)=\sum ^{}_{}x\cdot P(x)`

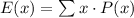
were x all the gains and P(x) their individual probabilities.

Then, the probability of getting a 6 is 1/6, the probability of getting a 5 is 1/6 and the probability of getting a 4 is 1/6, then the expected winnings for this game are:

`\begin{gathered} E(x)=6\cdot(1)/(6)+4\cdot(1)/(6)+1\cdot(1)/(6) \\ E(x)=(6)/(6)+(4)/(6)+(1)/(6) \\ E(x)=(6+4+1)/(6) \\ E(x)=(11)/(6) \\ E(x)=1.83 \end{gathered}`

The expected winnings are $1.83.